[프로그래머스][python3] 섬 연결하기

1. 문제 설명 및 분석

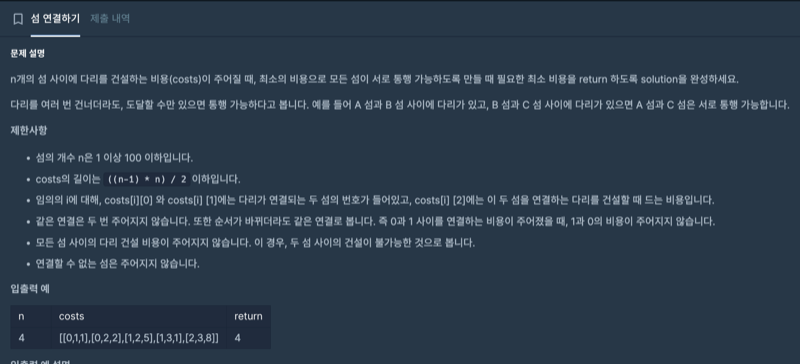
n개의 섬 사이에 다리를 건설하는 비용(costs)이 주어질 때, 최소의 비용으로 모든 섬이 서로 통행 가능하도록 만들 때 필요한 최소 비용을 return 하도록 solution을 완성하세요.

다리를 여러 번 건너더라도, 도달할 수만 있으면 통행 가능하다고 봅니다. 예를 들어 A 섬과 B 섬 사이에 다리가 있고, B 섬과 C 섬 사이에 다리가 있으면 A 섬과 C 섬은 서로 통행 가능합니다.

제한사항

• 섬의 개수 n은 1 이상 100 이하입니다.
• costs의 길이는 ((n-1) * n) / 2이하입니다.
• 임의의 i에 대해, costs[i][0] 와 costs[i] [1]에는 다리가 연결되는 두 섬의 번호가 들어있고, costs[i] [2]에는 이 두 섬을 연결하는 다리를 건설할 때 드는 비용입니다.
• 같은 연결은 두 번 주어지지 않습니다. 또한 순서가 바뀌더라도 같은 연결로 봅니다. 즉 0과 1 사이를 연결하는 비용이 주어졌을 때, 1과 0의 비용이 주어지지 않습니다.
• 모든 섬 사이의 다리 건설 비용이 주어지지 않습니다. 이 경우, 두 섬 사이의 건설이 불가능한 것으로 봅니다.
• 연결할 수 없는 섬은 주어지지 않습니다.

입출력 예

n	costs	return
4	[[0,1,1], [0,2,2], [1,2,5], [1,3,1], [2,3,8]]	4

2. 문제 해결

사고 과정

• 해당 문제는 최소 신장 트리(MST)를 찾는 과정으로 크루스칼(Kruskal) 알고리즘을 사용하면 해결할 수 있다.

코드 작성

# 순환을 방지하기위한 Union-Find 자료구조를 구현
def find(parent, x):
    if parent[x] != x:
        parent[x] = find(parent, parent[x])
    return parent[x]


def union(root_x, root_y, level, parent):
    # 트리의 레벨(높이)를 비교해 상대적으로 레벨이 낮은 트리를 높은 트리에 병합 
    if level[root_x] > level[root_y]:
        parent[root_y] = root_x
    elif level[root_x] < level[root_y]:
        parent[root_x] = root_y
    else: # 만약 동일한 레벨이라면 하나의 트리의 레벨을 상대적으로 높게 해 병합
        parent[root_y] = root_x
        level[root_x] += 1


def solution(n, costs):
    costs.sort(key=lambda x: x[2]) # 비용 기준으로 정렬

    count = 0
    total_costs = 0
    parent = [i for i in range(n)]
    level = [0] * n

    for x, y, c in costs:
        # 각 정점이 속해있는 트리를 찾는 과정
        root_x = find(parent, x)
        root_y = find(parent, y)

        # 다른 트리에 속해있을 경우 하나의 트리로 연결
        if root_x != root_y:
            union(root_x, root_y, level, parent)
            total_costs += c
            count += 1

        if count == n - 1:
            break

    return total_costs

제출 결과

3. 회고

• 특정 문제를 해결하기 위한 특정 알고리즘이 있다면 외워 두도록 하자.